Непознаваемость и неопределённость.

[maestro]

Мда... вот так всегда с ФаерСвордом. Хватает на 2 поста... До первого прихода модератора.

[FireSword]

И под занавес - вопросик, который выявит насколько хорошо Вы знаете
соотношение неопределенности. Для каких импульсов и координат оно не существует.
И второй вопрос - а для каких операторов (или величин) оно вообще существует. Это ведь тема нашего разговора, не так ли...


Я уже отвечал вам на него. Хоть вы и не поняли ответа. Принцип неопределенности явление наблюдаемое - существует не для операторов (явления не наблюдаемого, ибо существующего лишь в нашем воображении), а для массы и объема. Чем меньше исследуемый объем, тем большую массу виртуальных частиц там вполне реально - можно обнаружить.


Вообще-то, тебя уже никто не спрашивает - над тобой откровенно стебутся. Я просто приводил переписку, ты вырвал текст
из контекста, но да Бог с ним.

Читаем ссылку.

РСРёРЅСРёРї неопСеделСРЅРЅРѕСЃСРё РейзенбеСРіР° в Рикипедия

Вот, что в ней написано

В более общем смысле, соотношение неопределённости возникает между любыми переменными состояния, определяемыми некоммутирующими операторами. Это - один из краеугольных камней квантовой механики, который был открыт Вернером Гейзенбергом в 1927 г.

А Вот доказательство теоремы.

Обобщенный принцип неопределенности
Принцип неопределенности не относится только к координате и импульсу. В своей общей форме, он применим к каждой паре сопряженных переменных. В общем случае, и в отличие от случая координаты и импульса, обсужденного выше, нижняя граница произведения неопределенностей двух сопряженных переменных зависит от состояния системы. Принцип неопределенности становится тогда теоремой в теории операторов, которую мы здесь приведем
Теорема. Для любых самосопряженных операторов: A:H → H и B:H → H, и любого элемента x из H такого, что A B x и B A x оба определены (т.е., в частности, A x и B x также определены), имеем:
Это - прямое следствие неравенства Коши-Буняковского.
Следовательно, верна следующая общая форма принципа неопределенности, впервые выведенная в 1930 г. Говард Перси Робертсоном и (независимо) Эрвином Шредингером:
Это неравенство называют отношением Робертсона-Шредингера.
Оператор AB-BA называют коммутатором A и B и обозначют как [A,B]. Он определен для тех x, для которых определены оба ABx и BAx.
Из отношения Робертсона-Шредингера немедленно следует отношение неопределенности Гейзенберга:
Предположим, A и B две переменные состояния, которые связаны с самосопряженными (и что важно симметричными) операторами. Если ABψ и BAψ определены, тогда:
, где:
среднее значение оператора переменной X в состоянии ψ системы, и:
оператор стандартного отклонения переменной X в состоянии ψ системы
Приведенные выше определения среднего и стандартного отклонения формально определены исключительно в терминах теории операторов. Утверждение становится однако более значащим, как только мы заметим, что они являются фактически средним и стандартным отклонением измеренного распределения значений. См. квантовая статистическая механика.
То же самое может быть сделано не только для пары сопряженных операторов (например координаты и импульса, или продолжительности и энергии), но вообще для любой пары Эрмитовых операторов. Существует отношение неопределенности между напряженностью поля и числом частиц, которое приводит к явлению виртуальных частиц.
Возможно также существование двух некоммутирующих самосопряженных операторов A и B, которые имеют один и тот же собственный вектор ψ. В этом случае ψ представляет собой чистое состояние, которое является одновременно измеримым для A и B.

[править] Общие наблюдаемые переменные, которые повинуются принципу неопределенности

Предыдущие математические результаты показывают, как найти отношения неопределенности между физическими переменными, а именно, определить значения пар переменных A и B коммутатор которых имеет определенные аналитические свойства.

• самое известное отношение неопределенности между координатой и импульсом частицы в пространстве:

• отношение неопределенности между двумя ортогональными компонентами оператора полного углового момента частицы:

, где i, j, k отличны и Ji обозначает угловой момент вдоль оси xi.

• следующее отношение неопределенности между энергией и временем часто представляется в учебниках физики, хотя его интерпретация требует осторожности, т.к. не существует оператора, представляющего время:

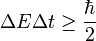Вот эта вещь назвается
коммутант и она выбрана так, что =0, если АВ=ВА. Надеюсь, ты еще помнишь, что АВ=ВА не для всех математических объектов так, а только для чисел. Да и то не для всех. Здесь же мы имеем матрицы, и АВ=ВА бывает крайне редко.

Такого красивого и обобщенного д-ва я еще не видел. А ты Википедю ругаешь! В Давыдове оно куда менее общо и обслуживает только интересы квантов. А тут, оно явно выходит за пределы квантовой механики. Хоть какая-то от тебя польза!

Да, если тебе Википедия, не нравится, читай Давыдова. Там все через скобки Пуассона. Ты не знаешь, че это такое... Ну это твои проблемы.
Тебя этому учили. Кстати, здесь тоже ничего сложного.
Неравенству Коши-Буняковского тебя учили на 2 семестре 1 курса -
в Линейной алгебре. Флаг в руки-с.

[FireSword]

М-дя... Я вообще-то оспаривал возможность измерения именно силы реакции опоры - именно она, а не вес действует на частицу!

Это тавтология, Файер. Вес это сила реакции опоры.

Отнюдь. Сила реакции опоры равна весу лишь по величине, но отнюдь не по направлению. По направлению - противоположна.
Смотри ссылку.

http://school.ort.spb.ru/(Eng)/library/physics/10class/machanics/lesson_4/lesson_4.htm

А вот, что в ней пишется.

(E - модуль Юнга, он зависит только от материала, из которого изготовлен упругий стержен (пружина))
Реакция опоры, вес тела.

Если тело лежит на опоре или весит на подвесе, то опора (подвес) деформируются.
Реакция опоры - сила упругости, которая возникает из деформации опоры или подвеса.
Реакция опоры - сила, которая действует на само тело со стороны опоры или подвеса.
Реакция опоры N перпендикулярна поверхности опоры.
Если тело лежит на опоре или весит на подвесе, то деформируется и само тело.
Вес тела - сила упругости, которая возникает из-за деформации самого тела.
Вес тела - сила, которая действует на опору.

По 3-му закону Ньютона реакция опоры равна по модулю весу тела и противоположна ей по направлению:

P=-N

Вес тела зависит от состояния движения тела и опоры.


Вес и сила реакции опоры - есть классическая иллюстрация 3 закона Ньютона. На это тему есть от шестой до четверти задач повышенной сложности в школьной физики. Выбанально не знаете 8 класса.
Чтобы проверить уровень Ваших знаний достаточно поднять старые школьные учебники. Это - где-то 18 век в науке. Начало века.

Короче, о весе, как и 3 законе Ньютона - ничегошеньки...
А как ты поступал на физфак... С таки знаниями ни в математ, ни в пед, ни в мед, ни на химию, ни на биологию. М-да!...

[maestro]

Кстати- сообщаю всем. Замечание снял я, поскольку пост месячной давности и в виде жеста доброй воли.

[FireSword]

Для Руллы.

Теперь по поводу того, что оператор не наблюдаем.
Собственные числа оператора наблюдаемы, да еще как!
В уравнение Шредингера для атома водорада собственное число оператора -R/n^2. Разница между энергоуровнями атома водорода
(R/n^2-R/m^2) и есть наблюдаемая величина.
п=1 - серия Лаймана.
п=2 - серия Бальмера
п=3 - серия Пашена
п=4 - серия Брикета
п=5 - серия Пфунда.

[FireSword]

Рулла, идите учить физику в библиотеку. Или напишите хоть одно уравнение квантов, в котором используется сила.

Смотрите выше. О чем и речь. То, что в квантовой механике понятие силы не используется, не является препятствием для измерения веса кванта.

А вес никакого отношения к квантовой механике ни имеет. Вес, повторяю, это сила давления на опору или сила, с которой закручивается подвес. Подвес и опора - тела всегда макроскопические.
(не менее несколько сотен атомов в длину). Экспериментатору надо ж как-то измерения проводить. Лебедев в свое время измерял именно
вес света (силудавления света на крылышки). И не про какую квантовую механику не знал.

Автор так и не объясняет как он собирается определить силу реакции опоры, действительно действующую на фотон. В опыте Лебедева

А описанный опыт никакого отношения к опыту Лебедева не имеет. В опыте Лебедева луч света перпендикулярен отражающим дискам и там речь, действительно, идет о давлении света. В описанном мною опыте луч параллелен чаше весов. И давить на нее не может.

Вес, опять напоминаю, это сила давления на опору или сила, с которой закручивается подвес. У вас наверное закручивается чашка.
То что фотон параллелен чашке - как раз для этого много ума прикладывать не надо. Только тогда P=mg. В других же случаях
P=m(g+a), a - ускорение торможения фотона. Это правда на языке
классической механики, которую здесь использовать можно не всегда.


Для особо неискущенных в физике читателей, поясню вес - это сила,
с которой тело давит на опору или закручивает подвес.

Надо же. Как далеко простирается ваша осведомленность.

Дальше твоей. И у Локки дальше. У него чашка не закручивается.
Вес - это сила с которым тело действует на другие тела...

На чашу весов, обычно. Как гамма-квант в описанном эксперименте.


На протяжении почти 2-5 страницы Рулла включает свой органчик,
и все время повторяет 1 и ту же фразу. Мол вес можно измерять.
Можно измерять, Рулла. Никакого, правда отношения к квантовой механике это не имеет. Чашка весов плохо похожа на фотон.

А вот измерька-та силу воздействия чашки на фотон. Или крышка весов Лебедева на свет. Или заряженной пылинки на электрическое или магнитное поле. Без использования 3 закона Ньютона. Он там не выполняется и использовать его там некорректно (измерять силу воздействия на чашку, и по ней - на частицу- запрещено, подходи с динамометром к фотону).

Весь прикол состоит в том, что измерять силу воздействия на тело, распростертое от - до + бесконечности, с постоянно меняющимся центром масс, невозможно.

И для этого не надо знать квантовую механику. Достаточно вспомнить воздействие реки на мячик (унее тоже меняется центр масс, и по сути она безразмерна). Измерь-ка силу воздействия мячика на реки.

Элементарная частица размазна по всей Вселнной точно так же, как
и река практически бесгранична.
Впрочем, иногда ее можно представить как шарик (гамма-квант, электрон в модели атома водорода и т.д.).

Если частица достаточно локализована (99% массы ее находится внутри маленького радиуса, для гамма-кванта - радиус ядра), то 1% размазанным поо остальной части вселенной можно пренебречь.
В этих случае допускается применение классической механики, но оно все равно будет неточным. Иначе - увы, Как в случае фотона радиочастот имеющего длину волны допустим 1 км, что бесгранично для чашки весов. Особенно ярко это проявлется при рассчете обменного взаимодействия, которое есть причиной ферромагнетизма, складывания маленьких магнитов в 1 большой домен с 1 направлением магнитного момета. Выделить силу там невозможно.


Итак, определите

1. Силу воздействия чашки весов на фотон (измерять, а не вычислять -
3 законом не пользоваться!).

2. Силу воздействия света на крылышко (измерять, а не вычислять -
3 законом не пользоваться!).

3. Силу воздействия пылинки на электромагнитное поле.

4. Силу воздействия мячика на реку.

Во всех случаях измерять, а не вычислять -
3 законом Ньютона не пользоваться!.

Даже 10 летним мальчишкам, известно, что базис в релятивистской теории и квантовой механике другой, чем в классической. В школе
(вообще-то!) проходят, что этот базис в классической - 3 закона Ньютона.

Ну и напоследок цитата.

Более того, в ряде разделов современной физики (например - в квантовой механике) понятие силы вообще исчезает, в то время как масса остается вполне определенной физической величиной. С этих позиций более предпочтительным является независимое введение массы тела. Однако, формулировка второго закона в виде утверждения о том, что сила равна произведению массы тела на его ускорение придает второму закону вид, характерный для математического определения, а не формулировки закона природы

База рефератов KENTOS.ru. Сила трения. Коэффициент трения скольжения

Это ссылка не самая супер, но примерно тоже можно найти в учебнике по квантовой механике, и даже в справочниках для поступающих в вузы.
Впрочем, не сомневаюсь, что ты воспользуешься, что не супер. Вот только найти это можно в любом учебнике по квантовой механике
и даже школьной литературе.

Вообще-то Рулла, это азы не квантовой механики, нет, а вступления в нее. Ну после непонимания базовых понятий веса, 2-3 закона Ньютона, диферренцирования меня ничего не удивляет. Ты Ревизора часом не читал, а...