Математическая задачка..
Свернуть
X
-
Не важно.
В задаче не сказано.
Важны две вещи.
Промежутки времени до обеда и от обеда до вечера одинаковы.
Производительность работы косцов одинакова и от времени не зависит.
Ну если у вас есть решение, то поделитесь им.
Просто ответы не принимаются.Последний раз редактировалось ilya481; 24 April 2021, 07:38 AM.Не может человек ничего принимать на себя, если не будет дано ему с неба. (Иоанн креститель)Комментарий
-
Только подготовленный Верой ум способен открыть
завесу буквы, скрывающую Истинное Знание.Комментарий
-
Не может человек ничего принимать на себя, если не будет дано ему с неба. (Иоанн креститель)Комментарий
-
Большое поле за день было выкошено полностью.
До обеда на нём работала вся артель, а после только половина.
Следовательно после обеда было скошено в два раза меньше, чем до обеда, то есть 1/3 большого поля.
1/3 большого - это 2/3 малого (при условии, что оно в два раза меньше).
И если оставшуюся треть малого поля один человек скосил за день (а это 1/6 за пол дня) , значит чтобы скосить две трети (или 4/6) за пол дня понадобилось 4 человека.
4 + 4 = 8Только подготовленный Верой ум способен открыть
завесу буквы, скрывающую Истинное Знание.Комментарий
-
Я думал так:
Решение:
Поскольку за день большее поле докосили 1+1/2 косцов , то 1/2 косцов докосило за полдня третью оставшуюся часть поля, ( в первую было тогда 2/3 большего поля) а всего таких частей было 1/3+2/3= 3/3.
Но мы знаем, что второе поле в два раза меньше, тогда всего частей: 3/3+1/2 =9/6
Теперь за полдня , скосили 2/3 большого поля, что составляет 4/6. За вторую половину скосили все косари тоже 4/6: Всего за день скосили 4/6+4/6=8/6
На второй день осталось: 9/6-8/6 =1/6 из 9/6
Теперь совсем простая арифметика: если один косит за день 1/6 частей, то чтобы скосить за день 8 этих частей нужно 8 человек."Никакое гнилое слово да не исходит из уст ваших... "(послание к Ефесянам 4:29)Комментарий
-
Алгебраически -
Х - кол косцов. У/2 - размер, который косит 1 косец за пол дня.
Размер большого поля до обеда
ХУ/2
Размер большого поля после обеда
Х/2У/2
Общий размер поля (ху)/2 + (ху)/4=(3ху)/4
Малое поле
Х/2У/2 + У =( ХУ)/2 + У
Уравнение
( 3ХУ)/4 =2 ( (ХУ)/2 +У )
У ( 3Х)/4= 2 У ( Х/2 + 1 )
3Х/4= 2( Х/2 +1)
3х= 4х+8
Х=8Комментарий
-
Не важно.
В задаче не сказано.
Важны две вещи.
Промежутки времени до обеда и от обеда до вечера одинаковы.
Производительность работы косцов одинакова и от времени не зависит.
Если 8-часовой рабочий день - то в артели 8 человек.
Ну если у вас есть решение, то поделитесь им.
Просто ответы не принимаются.
- это из задачника Перельмана..)
Артель косцов
Известный физик А. В. Цингер в своих воспоминаниях о Л. Н. Толстом рассказывает о следующей задаче, которая очень нравилась великому писателю:"Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру еще остался участок, скошенный на другой день одним косцом за один день работы. Сколько косцов было в артели?".
Рис. 6. Артель косцов
РешениеВ этом случае, кроме главного неизвестного - числа косцов, которое мы обозначим через х, - удобно ввести еще и вспомогательное, именно - размер участка, скашиваемого одним косцом в 1 день; обозначим его через у. Хотя задача и не требует его определения, оно облегчит нам нахождение главного неизвестного. Выразим через х и у площадь большого луга.
Луг этот косили полдня х косцов; они скосили - x × 1/2 × y = xy/4. Вторую половину дня его косила только половина артели, т. е. x/2 косцов; они скосили х/2 × 1/2 × у = xy/4.
Так как к вечеру скошен был весь луг, то площадь его равна xy/2 + xy/4 = 3xy/4.
Выразим теперь через х и у площадь меньшего луга. Его полдня косили x/2 косцов и скосили площадь x/2 × 1/2 × y = xy/4. Прибавим недокошенный участок, как раз равный у (площади, скашиваемой одним косцом в 1 рабочий день), и получим площадь меньшего луга: xy/4 + y = (xy + 4y)/4.
Остается перевести на язык алгебры фразу: "первый луг вдвое больше второго", - и уравнение составлено: 3xy/4 : (xy + 4y)/4 = 2, или 3xy/ (xy + 4y) = 2.
Сократим дробь в левой части уравнения на у; вспомогательное неизвестное благодаря этому исключается, и уравнение принимает вид 3x/(x + 4) = 2, или 3х = 2x + 8,
откуда х = 8. В артели было 8 косцов. После напечатания первого издания "Занимательной алгебры" проф. А. В. Цингер прислал мне подробное и весьма интересное сообщение, касающееся этой задачи. Главный эффект задачи, по его мнению, в том, что "она совсем не алгебраическая, а арифметическая и притом крайне простая, затрудняющая только своей нешаблонной формой". "История этой задачи такова, - продолжает проф. А. В. Цингер. - В Московском университете на математическом факультете в те времена, когда там учились мой отец и мой дядя И. И. Раевский (близкий друг Л. Толстого), среди прочих предметов преподавалось нечто вроде педагогики. Для этой цели студенты должны были посещать отведенную для университета городскую народную школу и там в сотрудничестве с опытными искусными учителями упражняться в преподавании. Среди товарищей Цингера и Раевского был некий студент Петров, по рассказам - чрезвычайно одаренный и оригинальный человек. Этот Петров (умерший очень молодым, кажется, от чахотки) утверждал, что на уроках арифметики учеников портят, приучая их к шаблонным задачам и к шаблонным способам решения. Для подтверждения своей мысли Петров изобретал задачи, которые вследствие нешаблонности очень затрудняли "опытных искусных учителей", но легко решались более способными учениками, еще не испорченными учебой. К числу таких задач (их Петров сочинил несколько) относится и задача об артели косцов. Опытные учителя, разумеется, легко могли решать ее при помощи уравнения, но простое арифметическое решение от них ускользало. Между тем, задача настолько проста, что привлекать для ее решения алгебраический аппарат совсем не стоит. Если большой луг полдня косила вся артель и полдня пол-артели, то ясно, что в полдня пол-артели скашивает 1/3 луга. Следовательно, на малом лугу остался нескошенным участок в 1/2 - 1/3 = 1/6. Если один косец в день скашивает 1/6 луга, а скошено было 6/6 + 2/6 = 8/6, то косцов было 8.Толстой, всю жизнь любивший фокусные, не слишком хитрые задачи, эту задачу знал от моего отца еще с молодых лет. Когда об этой задаче пришлось беседовать мне с Толстым - уже стариком, его особенно восхитило то, что задача делается гораздо яснее и прозрачнее, если при решении пользоваться самым примитивным чертежом (рис. 7)".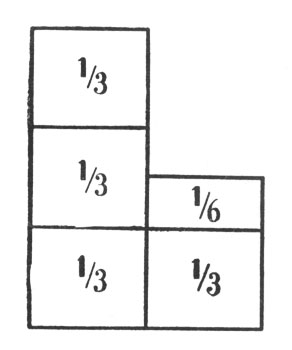
Рис. 7. Когда об этой задаче пришлось беседовать мне с Толстым - уже стариком, его особенно восхитило то, что задача делается гораздо яснее и прозрачнее, если при решении пользоваться самым примитивным чертежом
- - - Добавлено - - -
- да, Илья, благодарю!Да, конечно.
Признаюсь вам, я держал в уме это решение, но когда вы написали, что не надо алгебры (или я неправильно понял?), то я его отставил, ибо там нужна алгебра, пусть примитивная, но всё же.
Поэтому я склонился к решению Олега.
Но поскольку вы задали этот вопрос я вернусь к тому решению, которое у меня было запланировано сегодня утром.
По вашему рисунку длины красных отрезков (а их четыре) равны 28; а; в; 14
А ещё можно записать, что а+в= 45
А теперь складываем их (их длины) и получаем сумму двух полупериметров.
Т.е.
P1/2 +P2/2= 28+14+а+в = 28+ 14+ (а+в)= 28+14+45= 87.
Но мы знаем, что P1=P2 (по условию), поэтому сумма двух равных полупериметров равна одному полному периметру.
Ответ: P= 87
мы сейчас занимались, и вот это решение наиболее оптимальным показалось ребёнку, у Олега все-же более сложно,
но все решения были нам очень полезны!
мнс. кандидат наук... специалист по ядовитым змеям.
Задумайся кто ты, а потом рассуждай обо мне.
Комментарий
-
Оказывается, что важно.
1)Время до обеда и после обеда - равны друг другу.
2)Также продолжительность рабочих дней должна быть одинакова.
3)И также каждый труженик за рабочий день должен выкосить одинаковую площадь поля.
Это всё важно и истекает из сказанного в задаче.
Ну, вы же ставили условие, что задачу нужно решить не прибегая к алгебре,
вот я и попытался решить чисто логически и чисто практически.Последний раз редактировалось учащийся; 24 April 2021, 08:11 AM.... кто любит Меня, тот соблюдет слово Мое; и Отец Мой возлюбит его, и Мы придем к нему и обитель у него сотворим.
Межконфессиональный Христианский сайт и форум для желающих изучать БогословиеКомментарий
-
... кто любит Меня, тот соблюдет слово Мое; и Отец Мой возлюбит его, и Мы придем к нему и обитель у него сотворим.
Межконфессиональный Христианский сайт и форум для желающих изучать БогословиеКомментарий







Комментарий